Why Triple Integrals Are Actually Useful
You can feel the dread in a room when students realize double integrals and triple integrals exist. Integrals, which many students solely remember as “weird looking S things,” were already hard enough. In the 5 stages of math grief, the first is denial: they beg, “That’s a mistake right? Why are there two of those weird S’s?” After that is the second stage, anger: “When will we ever need to use this in real life!?” (The third stage is bargaining, where they ask me for the answers to their calculus test.)
I’m here to explain why we would need triple integrals (and integrals in general) in real life. When I first took multivariable calculus, I was also paralyzed with fear from the dreaded triple S, and I understand that at first the concept seems like abstract nonsense. But triple integrals are actually useful! We’re going to break this down first by going over why we need single integrals, then double integrals, then triple integrals.
How to Understand Single integrals
For simple shapes, we have neat formulas to find the area:

But how are we supposed to find the area of these shapes?

The answer is that we can use an integral. One simple way to describe an integral is that it’s the area underneath some curve, and usually we use the integral to find the area of weird shapes.
Say we want to find the area underneath a weird-looking curve that looks like this:

Measuring the exact area is tricky, so you might decide it’s a good idea to approximate the area under the curve instead.
As you rack your brain for a way to approximate the area, you might daydream about simpler shapes like rectangles. Ah yes, rectangles, with their easy-to-compute areas of height times width.
“Wait a minute,” you think, “Why don’t we approximate the area under the curve by drawing a bunch of rectangles under the curve, finding the areas of those rectangles, and adding all the little areas up, like this:”

This is a good idea, and a decent approximation. Our approximate area would be the sum of the areas of all the green rectangles.
Each rectangle will have the same width to make the calculations easier. The width is equal to an amount we’ll call Δx (conceptually, Δx is the change in x). The height is different for each rectangle, but it’s given by the function f(x), represented by the curvy black line on the top of the diagram.
To make it clear that the heights are all different, we can say the 1st rectangle from the left has a height of f(x₁), the 2nd rectangle a height of f(x₂), and so on. In general, the ith rectangle has a height of f(xᵢ).
The area of a rectangle is just height times width, so the area of one of the rectangles is equal to f(xᵢ)*Δx. If we sum up all the rectangle areas, we get an approximate area under the curve.
But our approximation isn’t that accurate — there are a bunch of gaps between our rectangles and the curve. We could make the approximation more accurate by increasing the number of rectangles, like so:
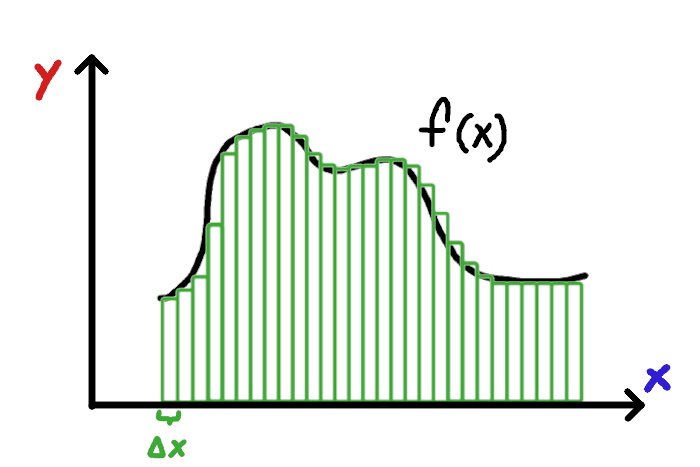
Notice that Δx, the change in x, is now smaller. Also, this sum is more accurate than the last. We can keep dividing the graph into thinner and thinner rectangles to make our sum even more accurate. Eventually, as the number of rectangles approaches infinity (and the width of each rectangle approaches 0), the approximate area gets closer to the actual area. What started as a rough approximation is now very accurate!
This sum is called an integral. An integral is written out like this:

The integral symbol ∫ looks like a big S, because when a German dude named Gottfried Leibniz developed calculus, he thought of the integral as an infinite sum. The “dx” represents Δx, the width of each rectangle, which is now infinitesimally small. The “dx” is called the differential. The f(x) is simply the same function as before (the black line).
So that’s how we use a single integral. We integrate over 1 variable, in this case x. As we move along the x-axis, we take the sum of a bunch of incredibly-thin rectangles. The smaller the width, the more accurate our approximation is. That’s how we find the area underneath the curve.
How to Understand Double Integrals
For 2-d shapes we have area, and for 3-d shapes we have volume. Like before, we have nice, neat formulas for the volumes of some 3-d shapes:

But finding the volumes of these 3-d shapes is much harder:

Needless to say, it’s not easy to find the volume of a dog, a sponge-looking thing, and/or some sort of blue deflated volleyball. How are we supposed to find the volume of these weird shapes? To find the volume we’ll use a double integral.
Let’s say I want to find the volume of this loaf of pineapple bread:
Like before, we can start by approximating the volume. Instead of dividing the graph into rectangles, we could start by dividing this chunky loaf into slices along the y-axis:

Each slice has the same width; let’s call that width Δy. If we add up the areas of all the slices, we get an approximate volume of the loaf. And like before, as we divide the loaf into thinner and thinner slices (as Δy gets closer and closer to 0), the approximation of the loaf’s volume gets more and more accurate.
So we just have to add the areas of all the bread slices. The only problem is, calculating the volume of a bread slice is not that easy. If we look at an individual slice, you’ll notice it’s kind of a weird shape itself:
We need to approximate the area of this bread slice, and we can do that by dividing it into a bunch of rectangles. In other words, to find the area of one slice, we have to perform a single integral like in the last section:

To find the area of one bread slice, we integrate over the x-axis, adding up tiny rectangles. Then, going back to the loaf, we integrate over the y-axis to add up the areas of all the slices.
Essentially, to find the volume of the pineapple bread loaf, we take an integral of integrals: we take a sum of slices, where each slice itself is a sum of rectangles. Of course, “integral of integrals” is clunky to write, so we just call this a double integral, and we write it like this:

The “dy” is the width of a bread slice (since each slice is along the y-axis), and the “dx” is the width of a rectangle within a bread slice (since each rectangle within a slice is along the x-axis). The f(x,y) refers to the top of the loaf. This is because the height of the loaf at some point (aka the z-coordinate) is a function of that point’s x-coordinate and y-coordinate, so it’s f(x,y).
How to Understand Triple Integrals
Alright, now we’re at the fun part: triple integrals. We’ve already covered single and double integrals. Hopefully, it’s clear why these can be useful: while it’s not their only use, they can help us find the areas and volumes of irregular 2-D and 3-D shapes!
You might guess that there’s a pattern here that goes something like this:
- With single integrals, we integrate over one dimension to find the area of a 2-dimensional shape.
- With double integrals, we integrate over two dimensions to find the volume of a 3-dimensional shape.
- With triple integrals, we integrate over three dimensions to find the volume of… a 4-dimensional shape?
And you would be right! A triple integral is used to find the volume of a 4-dimensional shape. This sounds impossible. “We don’t live in 4-dimensional space, Mark” you might say. “How can these be useful when 4-dimensional shapes don’t exist!” Well first of all, my name is Mike, not Mark. But second, I can explain how triple integrals are useful in the real world. To see this, we need to change the way we think about dimensions.
How Many Dimensions are in a Photo?
Let’s go back to double integrals for a moment. Have you ever seen a thermogram? It’s one of those photos made with a thermal camera, where different colors represent different temperatures. The cover of Brockhampton’s album Iridescence is a thermogram. There’s also this thermogram of a cat.
Photos are 2-dimensional, but every point on a thermographic photo has a “heat” associated with it. Since heat is measured numerically (with temperature), we can accurately say that every point on a thermographic photo has a number associated with it:

As you can see from the legend on the right, the blue spots may have a heat value of “15,” and the redder spots might have a value of “28.”
We can even turn this photo a 3D plot, where the height (z-coordinate) corresponds to heat (so a 30-degree-spot in the photo will be taller than a 15-degree-spot):

So here’s a question: how would I find the total amount of heat over this entire photo? The answer is that we use a double integral! We integrate over the x-axis and y-axis, and sum up the temperature throughout the photo. The total amount of heat is equal to the volume of the 3D plot above.
That may seem confusing, since the photo is 2-D, and as mentioned before, double integrals are used to find the volume of a 3-dimensional shape. But we need to change how we think of “dimensions.” We usually think of dimensions as spatial dimensions: in your kitchen you can move around in 3 spatial dimensions. However, a “dimension” really just refers to a value associated with a point. A dimension does not have to be a direction in space. For example, take a look at this graph of the number of flight passengers from 1949–1961:

This bar graph has two dimensions, but they’re not quite x and y. The two dimensions are “Date” and “Passengers,” and it just so happens that the date is plotted along the x-axis and the number of passengers is plotted along the y-axis.
In the thermogram, there are 2 spatial dimensions, as well as a 3rd dimension of heat. Heat is the secret 3rd dimension, which means we can treat the photo as a 3-D object and use a double integral.
Triple Integrals in the Real World
Okay, so back to triple integrals. Let’s say you have a bedroom that’s shaped like a box. The heating vent may only be in one corner of the room, so the heat is not evenly spread throughout your room. The temperature will be high near the vent, low in the opposite corner from the vent, and so on. The heat at any given point in the room is given by some function f(x,y,z) (it’s a function of the x, y, and z-coordinates of some point in the room).
If I want to add up all the heat in the room, how would I do that?
Clearly, there are 3 spatial dimensions in the room. But again, temperature also counts as a dimension, since it’s a number associated with a point. So this problem takes place in 4 dimensions: width, length, height, and temperature.
Since there are 4 dimensions, we would use a triple integral!
Let’s start by visualizing the room. This is what a 3-D thermogram of a 3-D room could look like:

As said before, if you look at the box, temperature is a function of a point’s exact x,y, and z-coordinates within the box. This function is f(x,y,z).
We’ll start by integrating over the z-axis, dividing the box into lots of slices parallel to the ground:

At first, it might seem like I split the room into a bunch of 2-D slices, but remember, temperature is also a dimension. I actually took the room and sliced it into a bunch of 2-D thermograms. And as we went over, a 2-D thermogram can be turned into a 3-D plot:

Next, we’ll integrate over y, dividing the thermogram into lots of little slices, like we did with the pineapple bread loaf:

Finally, we’ll take each slice and divide it into lots of little rectangles along the x-axis:

By doing this, we can accurately add up all the heat in this boxy room. We split the room into thermograms along the z-axis, then we divide the thermograms into slices along the y-axis, then we divide the slices into rectangles along the x-axis. We take a sum of sum of sums, an integral of integrals of integrals (good luck saying that 3 times fast). We call this the triple integral. It’s written like this:

The “dz” is the change in z, the “dy” is the change in y, and the “dx” is the change in x. The function f(x,y,z) is the function that tells you the temperature of some point in the room.
Using this triple integral, we can find the total amount of heat in the 3-dimensional room. If a “dimension” can mean something other than a spatial dimension, we realize there are lots of applications for triple integrals. We could find the total inertia over some 3-D object, or the gravitational pull on a basketball.
Conclusion
In short:
- A dimension, for math purposes, does not have to refer to space. It can refer to any numerical value, such as temperature, inertia, or humidity.
- In a single integral, we integrate over 1 variable to find the area of a 2-D shape.
- In a double integral, we integrate over 2 variables to find the volume of a 3-D shape.
- In a triple integral, we integrate over 3 variables to find the volume of a 4-D shape.
So yes, we use triple integrals to find the volume of 4-dimensional shapes, which sounds useless at first. But it only takes a shift in the way we think about “dimensions” for us to see that 4-D shapes are more common than it seems. Triple integrals help us make sense of those shapes and understand them.
That’s why triple integrals are useful.
